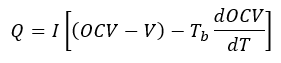Results
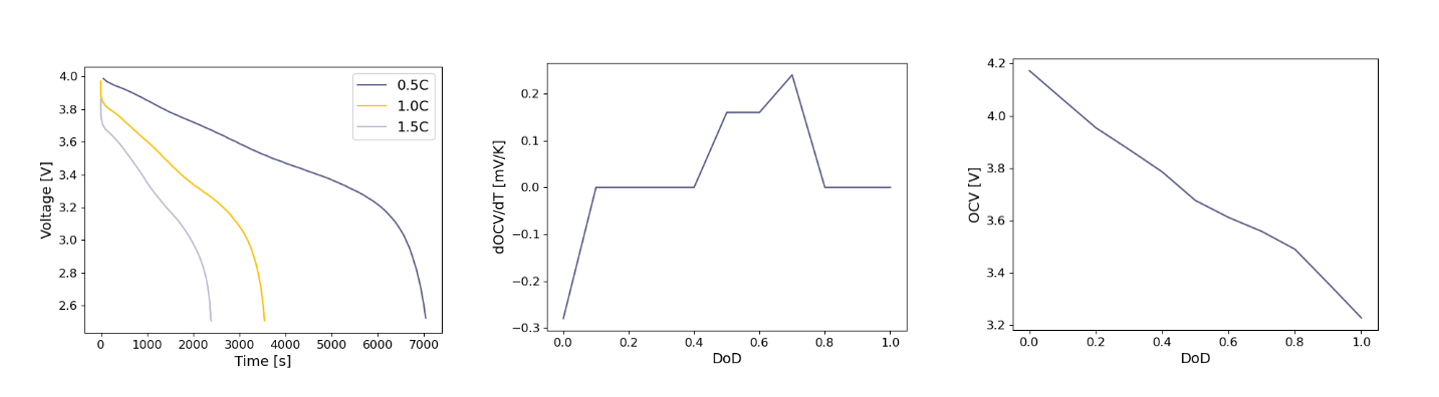
Three different discharge rates have been simulated to be compared to the test data. The discharge rates are 0.5C (I = 1.625A), 1.0C (I = 3.25A), and 1.5C (I = 4.875A). In the three plots below the temperature increase of the batteries over time is given and compared to the experimental data. In this plot it is visible that a reasonable comparison can be made for 1.0C and 1.5C but the difference is quite large for a discharge rate of 0.5C.
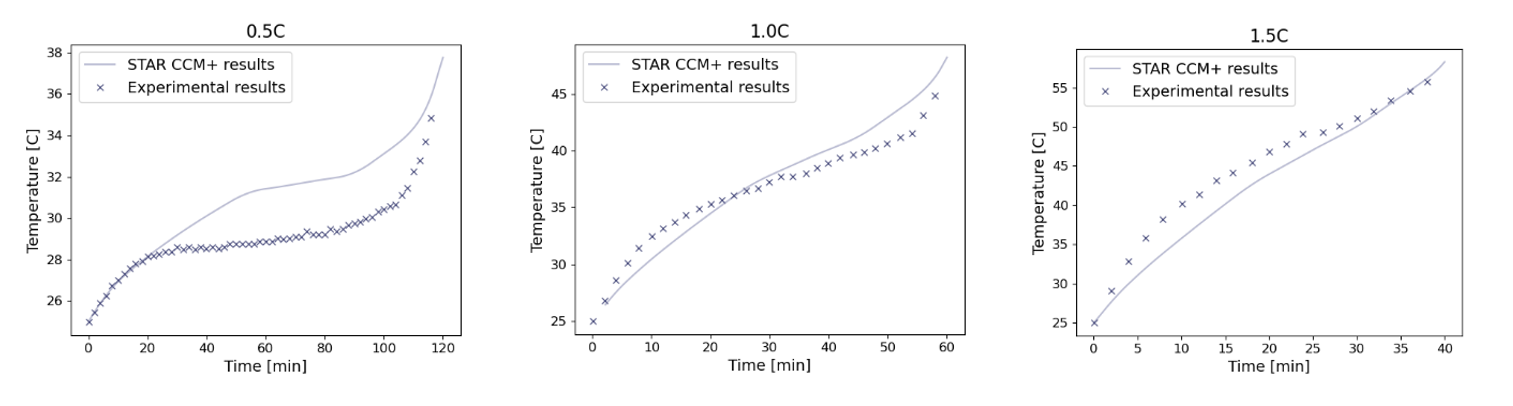
Figure 4: Experimental results versus simulation results
In the table below the error in temperature at the last (measured) timestep and the maximum error is given. From this table it can be concluded that the best overall fit is found for a 1.0C discharge rate. The error for the final temperature is at most 3.5%, while the maximum error within the domain is found for the 1.5C discharge rate with an error of 11.6%.

Table 2: Results
In the three plots below, the temperature increases over time compared to the experimental results can be seen. However, this time the heat production, Q, is added on the right axis. From the heat production it can be seen that the CFD simulation has the tendency to react slower to changes in the heat production compared to the test.
Especially with a discharge rate of 0.5C this causes the flat part of the curve (between 40 and 100 minutes) of the simulation to lie at a much higher temperature compared to the test. However, this also causes the low error in the final temperature, because the slope of the curve is lower at the end for the simulation compared to the test.
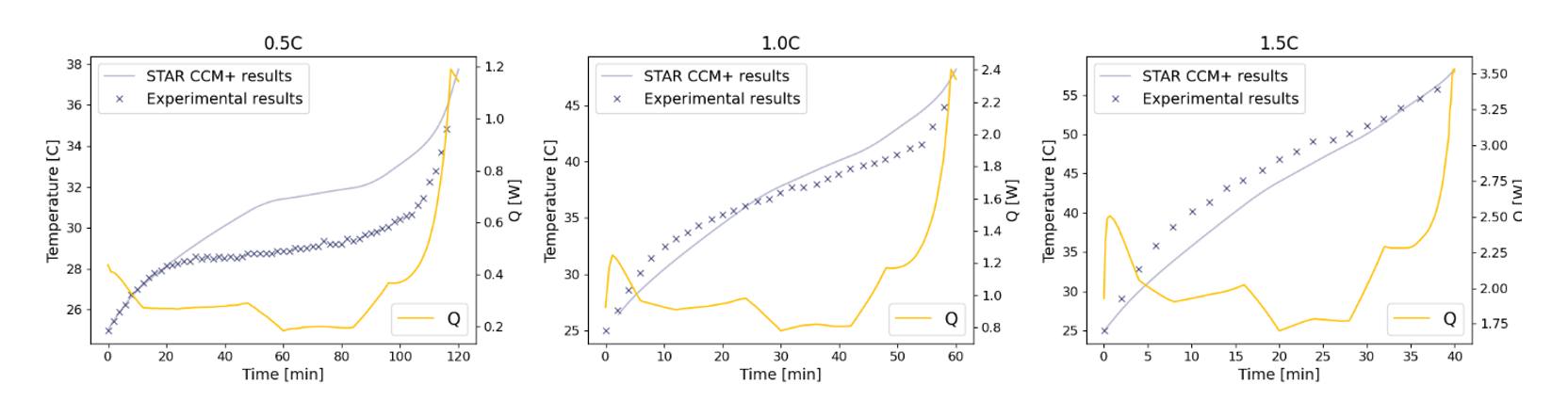
Figure 5: experimental results with simulation results, with the addition of the heat generation