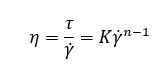Most everyday fluids can be considered Newtonian fluids. This means that the shear stress that occurs within the fluid is linear with the amount of shear strain rate. For example, the faster you would rub the palm of your hand over a fluid element, the more you will endure resistance, through the shear stress of the fluid.

However, for non-Newtonian fluid it can either become easier to move your hand over the fluid element or it can become much harder. The first one is called shear-thinning and the second is referred to as shear-thickening. A good example of the first one is ketchup, which is nearly solid, until the shear stress is sufficient, and it starts flowing. For the second one, look at custard/oobleck, which is normally runny but can be hard enough to run on if you stamp (if you stop, you sink!). In fluid flows, the hand is replaced by fluid element(s) that are adjacent to the fluid element considered, thus the fluid elements are exerting shear stresses on one another.

To simulate a non-Newtonian fluid, an equation to relate the shear stress (denoted by τ ) and the shear strain rate (denoted by ̇γ) is required. In our analyses, we used a so-called power law:

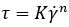
In this function, K is a constant factor and n is the exponent which determines the effect of the shear strain rate on the shear stress. For n=1, we automatically obtain a linear relation, which indicates a Newtonian fluid. When n<1, the shear stress increases initially but then tapers off with increasing strain rate (for example the ketchup described above). For n>1, the increase in shear stress keeps growing with higher strain rates, more than it would for the Newtonian equivalent (for example the oobleck described above). The variation for the shear stress as well as the viscosity can be found in the figure below, for different values of n.

Perhaps a more intuitive way of looking at it, is through the viscosity (right plot above). Honey is thicker for example and has a higher viscosity than water. The viscosity can be related to shear stress and shear strain rate through:

Again, when n=1, the viscosity will be constant η=K , as expected for a Newtonian flow. When n<1, the viscosity decreases with the shear strain rate. In other words, the fluid could start as thick as honey but end up as water, when a force is applied. When n>1, the opposite happens.

To simulate vla in STAR-CCM+, the power-law model was used, and a simple cylindrical test domain was employed where the substance enters through a small hole at the top. This simulation setup lends itself well for varying the parameters of the power law model, K and n. Through literature (source: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5976603/), it was found that yoghurt typically has a K of 1.54 and n of 0.82. Since vla is a shear thinning fluid, it was chosen to vary both parameters and compare the results. This shows that the parameters resembling vla the closest are most likely K=30 and n=0.8.