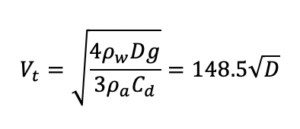Rain

Before starting the simulation to simulate any rain we need to know something about the rain, such as the average droplet size and the type of rain we want to model (light, moderate, heavy or even violent). To show a nice amount of rain in a short video we chose to go with heavy rain, simulating 750 droplets per second, which amounts to almost 15mm of rain an hour. Another part that is needed to model rain is the size of the particles. Average rain particles are about 2.5mm in size with minimum and maximum values of about 0.6mm and 5mm

Physics

Since we are modelling both water and air, we need a Multiphysics model in this case. However, in this simulation we want to model two things; we want to model the droplets in the air and we want to model the water droplets sliding off an object (in this case an umbrella).

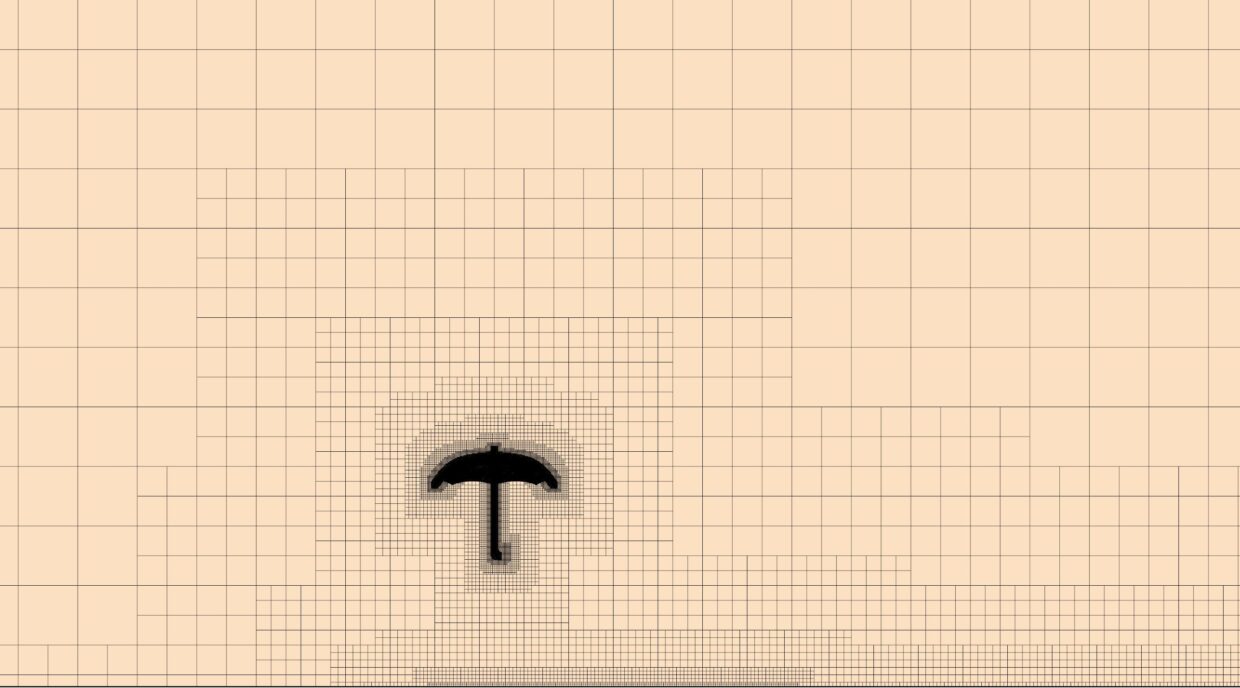
To model the droplets sliding off an umbrella we would like to use the Eulerian Volume of Fluid (VOF) multiphase method. However, to model the droplets in the air with this method we would need a mesh size at most as big as our smallest droplet and preferably a little smaller. This would lead to enormous mesh sizes causing the calculation to run for weeks or even months. For the droplets itself we would thus preferably use the Lagrangian method. The Lagrangian method follows the particles itself (which are called parcels) and solves the equations for each parcel. The size of the parcel is mesh independent; thus we can use a coarse mesh but still add small parcels (such as our rain droplets with sizes between 0.6mm and 5mm).

We now defined the two multiphase models we would like to use, but we would like to use them in combination: Lagrangian for the droplets and Eulerian VOF for the rain on the umbrella. Luckily it is possible in Simcenter STAR CCM+ (2020.3) to use impingement, where Lagrangian particles are changed to VOF when the Lagrangian particles reach a certain size (such as when they spread out on a surface). Once the VOF water phase then reaches the end of the umbrella the small droplets coming off the umbrella will again be changed to Lagrangian particles to continue their fall towards the ground.

By combining the two methods we only have to create a small mesh on our umbrella, all other regions can be modelled with a coarse mesh. This allows us to solve the simulation much faster.

Initial conditions

Since for Lagrangian particles the equations are solved for each parcel we want to keep the amount of parcels as small as possible, since more parcels means longer simulation times. Therefore, to both reduce the size of the domain and the amount of particles in the domain, we give each particle an initial (terminal) velocity based on its diameter. This way we don’t have to make the domain high enough for the particles to reach terminal velocity, decreasing the simulation time and the amount of particles in the domain.
The equation used to calculate the terminal velocity V_t of a falling rain droplet is as follows, where a drag coefficient (C_d) of 0.5 is assumed.

Where ρ_w is the density of water, the diameter of the particle, g the gravitation acceleration and ρ_α the density of the air the particles move through. The maximum and minimum velocities are shown in the image below. Since the particle diameter is distributed through a normal distribution it is possible that no particle of maximum size is present in the domain. Thus, the maximum velocity changes from timestep to timestep.  The minimum size of the raindrops can change between the input minimum size and the minimum size of the raindrops coming off the umbrella. For the drag the schiller-Naumann correlation is used to make sure that the velocity of the raindrops does not keep on increasing while falling.

To simulate the randomness of rain the injected particles of the Lagrangian phase are randomized both over every timestep and over area. Thus, not every timestep has the same amount of particles, and not every square meter on the injection site has the same amount of particles, leading to more random rain than when this was not the case.
The small domain in combination with the initial velocity causes the amount of Lagrangian particles to stay below 1000. This means that instead of having a domain with very small mesh-cells, increasing the simulation time significantly, we can use instead a domain with large mesh-cells and only a maximum of a 1000 Lagrangian particles.

Combining all that is described in this article leads to the final video below:
STAR-CCM+ is well capable of simulating a wide variety of flows and provides techniques for decreasing the time it takes to run a simulation. Shown here is a simulation of rain falling on an umbrella. The results show that a realistic solution is achieved.